In this post, we will continue addressing the quantitative aspect of application security. I recently focused on the KPIs of the vulnerability management process (in my post here), and now I will concentrate on the evaluation of a specific product. As an engineer with a long past in research, I'm kinda of measurement addicted. Indeed, measuring things is the easiest and only way we have to move toward factual, quantitative, and data-driven cybersecurity. While securing our infrastructure and processes, we move in two directions. One serves to make sure the arsenal of solutions we have within our hands is large enough to cover the whole range of challenges and tasks we may have to face. The second serves to know how well each solution is performing. It investigates facts like the core ruleset of ModSecurity being able to spot at most 70% of the attacks generating up to 1% of false alarms, or evaluating if 5% of false alarms are or not a good performance for a SAST scanner.
And, above this, do you have an even rough estimate in terms of detection capability and false alarms produced by the tools in your AppSec environment?
In this post, we will dive into the evaluation of the performance of AppSec solutions, covering three areas:
explaining the metrics that are commonly used to evaluate the tools;
explaining ROC curves, which are a widely used representation to
introduce the OWASP Benchmark project, which is a Java test suite designed to evaluate the accuracy, coverage, and speed of automated software vulnerability detection tools.
We will concentrate in this post purely on the classification capabilities of a solution, leaving purposely outside the analysis of other qualitative aspects like usability, degree of automation, integration with third-party solutions, or finally the hardware resources required, which may yet have a relevant role in a comprehensive evaluation of a solution.
Cybersecurity as a binary classification problem
What cybersecurity is about, in essence, is the capability to spot the malicious items that might threaten our data and systems, or if there is any safety implication, even impair people using them. While doing so, we want "ALL and ONLY" the malicious patterns to be labeled as such. That "ALL and ONLY" means two things: one is that no malicious pattern should pass undetected (the "ALL"), and at the same time no legitimate patterns should be labeled as malicious (the "ONLY).
Seen from a broader perspective, this means that a cybersecurity product solves a binary classification problem, where the item analyzed (independently from being lines of code, HTTP requests, IP addressed, or something else) are assigned either to the class of legitimate or malicious items. Since cybersecurity products are tailored to spot attack instances, the class of attacks is usually referred to as the positive class, whilst that of the legitimate items is the negative one.
The class assigned by the product to each pattern analyzed must be compared against the real nature of the object, which can be, again, legitimate (negative) or malicious (positive).
Thus, four different situations may occur:
a malicious (positive) pattern is classified as malicious (positive);
a malicious (positive) pattern is classified as legitimate (negative);
a legitimate (negative) pattern is classified as malicious (positive);
a legitimate (negative) pattern is classified as legitimate (negative).
We want of course the number of patterns falling in situations 1 and 4, which correspond to the right classifications, to be as high as possible, whilst those in situations 2 and 3, should be as low as possible as they represent a wrong decision.
Said differently, once an alert occurs, it might be due either to a real attack spotted by the system or to a wrong decision which leads the system to classify as malicious a patter which is instead legitimate. From this perspective, it becomes straightforward to measure the performance of systems based on two criteria:
one is the true positive or detection rate, which represents the fraction of malicious patterns classified as such;
the second is the false positive or false alarms rate, which represents the fraction of legitimate patterns erroneously classified as malicious.
The behavior of such binary classifier is generally not static and can be adjusted via a tunable threshold: playing with such threshold, we move from a poorly aggressive detection (which generates low false positives) to the most aggressive behavior where the detection rate is maximum but false positives might be also.
There might be cases where we do not have the chance to act directly on the threshold, but we can play with it only indirectly. A practical example is represented by the Paranoia Level (PL) in the OWASP Core Rule Set. PL is a configuration parameter used to select which rules are enabled to analyze the HTTP requests. CRS includes four PLs (PL1 - PL4) and each rule is assigned to a specific PL. Specifically, rules are grouped by PL in a nested way: when setting a certain PL, it enables all the rules assigned to this PL as well as those assigned to lower PLs.
A full evaluation of a solution should consider all the possible thresholds and consequently consider the corresponding false positive and detection rates.
Once this, we have the chance to represent and evaluate the performance of the tools via ROC Curves.
Visualizing the full range of performances of a system: the role of ROC Curves
A Receiver Operating Characteristic (ROC) curve is a graphical representation of a classifier's performance across various thresholds. Formerly introduced by electrical engineers and radar engineers during World War II for detecting enemy objects on battlefields, they are nowadays widely used to analyze the performance of binary classifiers. A ROC curve illustrates the trade-off between the True Positive Rate (TPR) and False Positive Rate (FPR) for different threshold values.
To create an ROC curve, a classifier's output, typically a probability score, is sorted, and a threshold is applied to determine positive and negative classifications. As the threshold varies, TPR and FPR change, resulting in a curve that often resembles an ascending diagonal line.
A perfect classifier would have a ROC curve that reaches the upper-left corner (TPR = 1, FPR = 0) with an area under the curve (AUC) of 1. An AUC of 0.5 represents a classifier that performs no better than random chance (i.e., a straight diagonal line). Such a diagonal line is also called an Equal Error Rate (EER) line, and represent the point where the false and the true positive rate stick to the same value.
Said differently, working points above the EER line are better than random guesses, whilst those below are worse than random guesses.
In cybersecurity applications, it is also frequent that not the whole ROC curve is considered, but only the portion that stands within a given range of false positive values. This generally helps to have a much more precise representation of how the system works within a range of thresholds and consequent false positive values which are acceptable in practical use. A maximum of 1% or 10% are widely used upper bounds for this kind of evaluation. In such a case, we can't consider 1 as the value of the AUC of an ideal classifier but we have instead to reduce the reference value proportionally to the maximum false positive rate. For instance, if 10% is the maximum false positive rate allowed, we shall consider only 10% of the whole AUC, and the reference value for an ideal classifier is 0.1. In literature, such a fraction of the AUC is usually referred to as "partial AUC".
But why use ROC Curves in Cybersecurity?
Applications can be manyfold. First, ROC curves allow cybersecurity to compare different models or solutions by assessing their AUC values. A model with a higher AUC generally exhibits better discrimination between legitimate and malicious activities. Second, ROC curves help in choosing an appropriate threshold that balances TPR and FPR based on specific cybersecurity goals. For instance, in some cases, minimizing FPR is crucial, while in others, maximizing TPR is more important. ROC curves provide the representation of the full range of performance of a solution, enabling thus to identify the most convenient working point. Third is monitoring and adaptation: as the environment monitored by the solutions is not static but instead evolves, a periodic re-evaluation based on ROC curves can assist in monitoring a system's performance and making adjustments when necessary, such as recalibrating thresholds or updating the classifier.
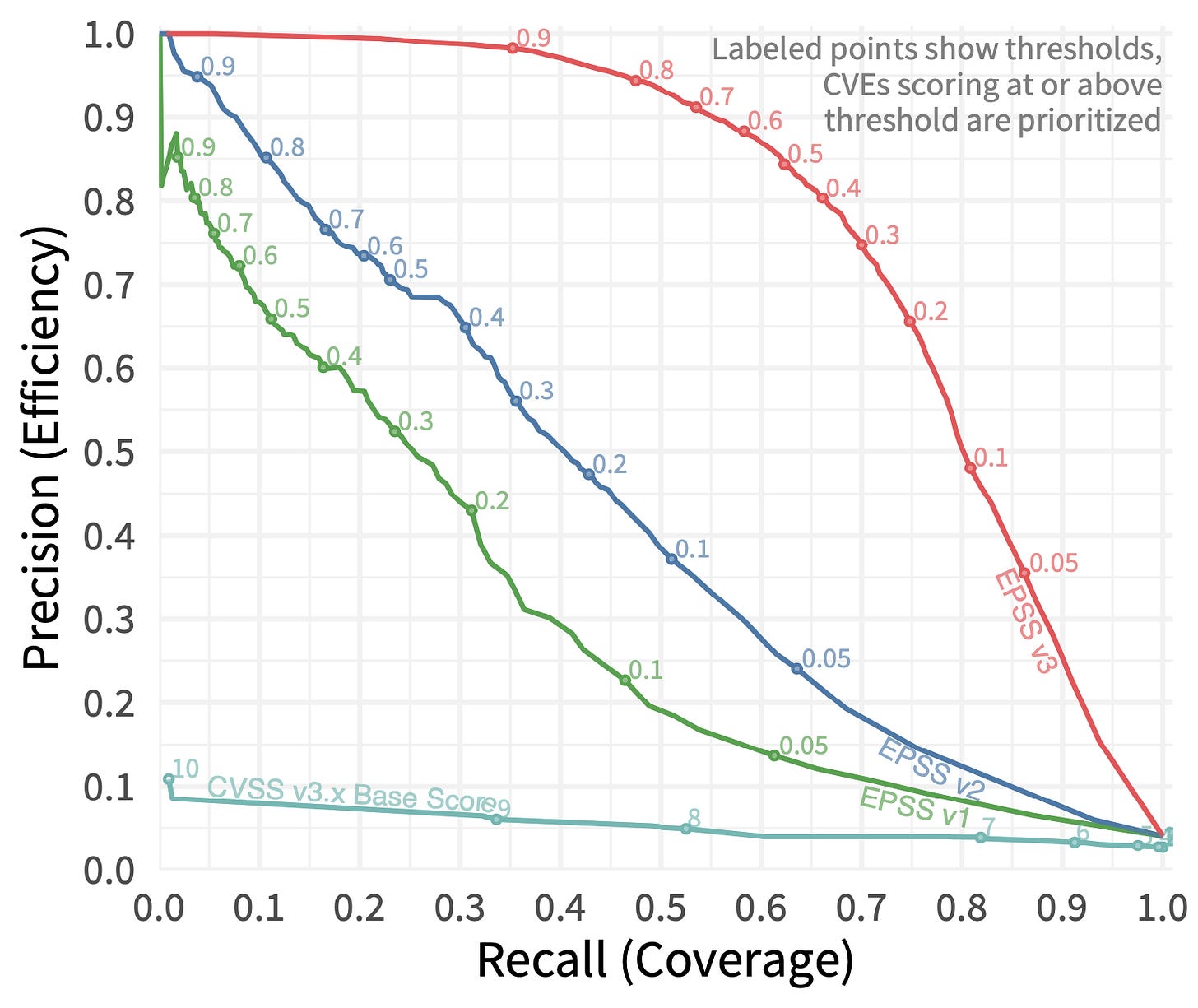
A good example of using ROC Curves is provided in the paper which introduces the Exploit Prediction Scoring Systems. Versions from 1 to 3 of EPSS are compared against each other and CVSS 3.x, in terms of efficiency and coverage (I have explained efficiency and coverage here). The plot clearly shows how performance gets better progressively the ROC curve approaches the upper right corner and the AUC tends to 1.
Getting the performances assessed: the OWASP Benchmark project.
Now that we have analyzed the methodological framework for evaluating the tools, we need to take a final step and identify a benchmark on which to measure the performances as described above. There is a nice OWASP project that helps with this, and it is the OWASP Benchmark project.
The OWASP Benchmark serves as an open-source web application equipped with thousands of exploitable test scenarios, each associated with specific CWEs. It's designed for analysis by various Application Security Testing (AST) tools, including but not limited to SAST, DAST (such as OWASP ZAP), and IAST. The goal is to ensure every vulnerability intentionally added and evaluated by the Benchmark is genuinely exploitable, offering an even-handed assessment for any application security detection tool. Additionally, the Benchmark encompasses numerous scorecard creators for a wide range of both open-source and proprietary AST tools, with its support list expanding continuously.
Version 1.2 which is the current version of the application covers 2,740 tests, associated with 11 different CWEs.
Each benchmark version comes with a spreadsheet that lists every test case, the vulnerability category, the CWE number, and the expected result (true finding/false positive). Part of the project is also the generation of scorecards, which represent the performance of the tools in terms of false positive and true positive rates. Scripts are provided that analyze all the tool scan results in the /results folder as compared to the expected results file for that test suite and generate a scorecard for all those tools in the folder.

References
The partial area under the summary ROC curve - https://pubmed.ncbi.nlm.nih.gov/15900606/
OWASP Benchmark Project - https://owasp.org/www-project-benchmark/
Enhancing Vulnerability Prioritization: Data-Driven Exploit Predictions with Community-Driven Insights
How CRS Works - https://coreruleset.org/docs/concepts/paranoia_levels/#:~:text=It%20is%20always%20possible%20to,to%20introduce%20more%20false%20positives.